消失的青年失业率：时间序列预测青年失业率

前言

面对预计将连续第七个月上升的青年失业率，在 2023 年 8 月 12 日统计局宣布停止青年（19-26 岁）失业率，被批判“掩耳盗铃”，而且在统计规则中一周工作一小时及以上属于就业，尽管数据上“注水”，但其变化仍然能反映现实失业的情况。

实际上数据上涨本身自然能降低社会对经济的预期，但本文通过时间序列预测未来 200 日失业率，从周期性、季节性得出，8 月为青年失业率的周期性高峰且见顶，选择不公开有利于经济预期的调整。

注：本文撰写时间为 2023 年 8 月 20 日，正待未来的经济数据来验证我的想法和预测，算是个自然实验。

全景

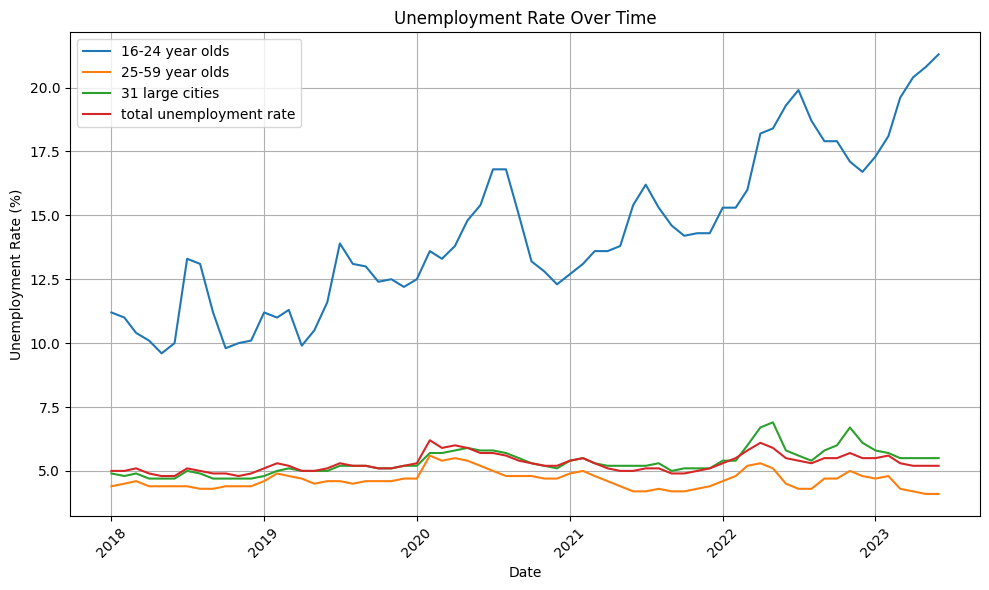
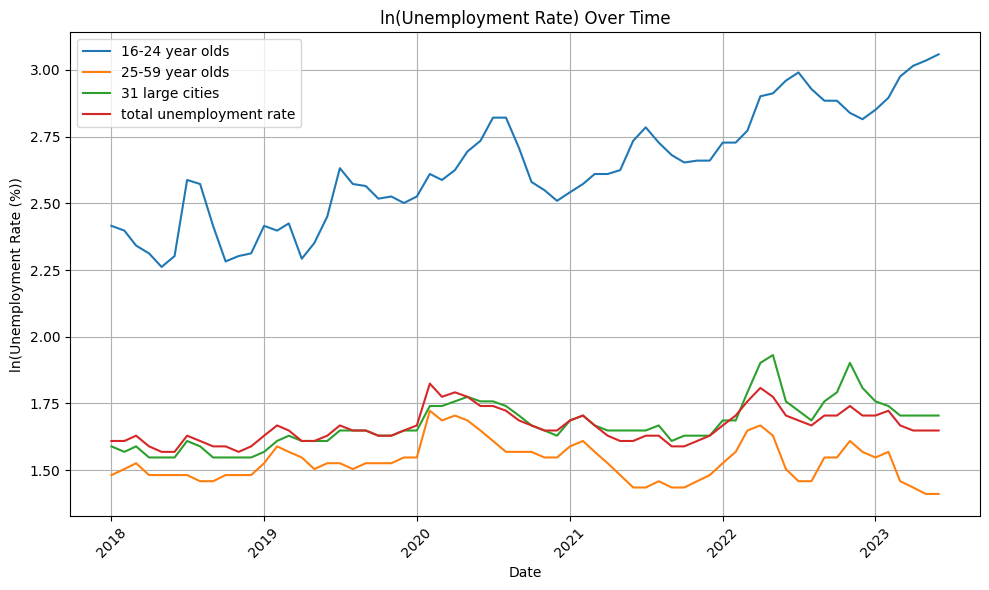
1. 25-59 岁的差距率在 2020-2022 年疫情后首次拉开差距，并逐渐扩大，就业市场更倾向于拥有一定工作经验的群组，企业经历了从扩张期到存量市场竞争，大企业裁员和招聘冻结，说明经济预期本身在影响企业的决策。

2. 每次失业率上涨的趋势，31 个大城市的失业率上涨更多，说明大城市的就业市场更不稳定，但回落又很快回到总体失业水平，说明大城市的人员流动性充足。

3. 青年失业率在 2018 年前都在 10%左右波动，长期青年失业背后是结构性失业而非周期性的。

为了过滤周期性和季节性使用 Prophet 时间序列预测未来的青年失业率：

from prophet import Prophet


df_y = df.reset_index()[["date", "National urban survey unemployment rate for 16-24 year olds(%)"]].rename(
    columns={"date": "ds", "National urban survey unemployment rate for 16-24 year olds(%)": "y"}
)

model = Prophet(interval_width= 0.95)
# 95% interval width

# Fit the model
model.fit(df_y)

# create date to predict
future_dates = model.make_future_dataframe(periods=6,freq="M")

# Make predictions
predictions = model.predict(future_dates)

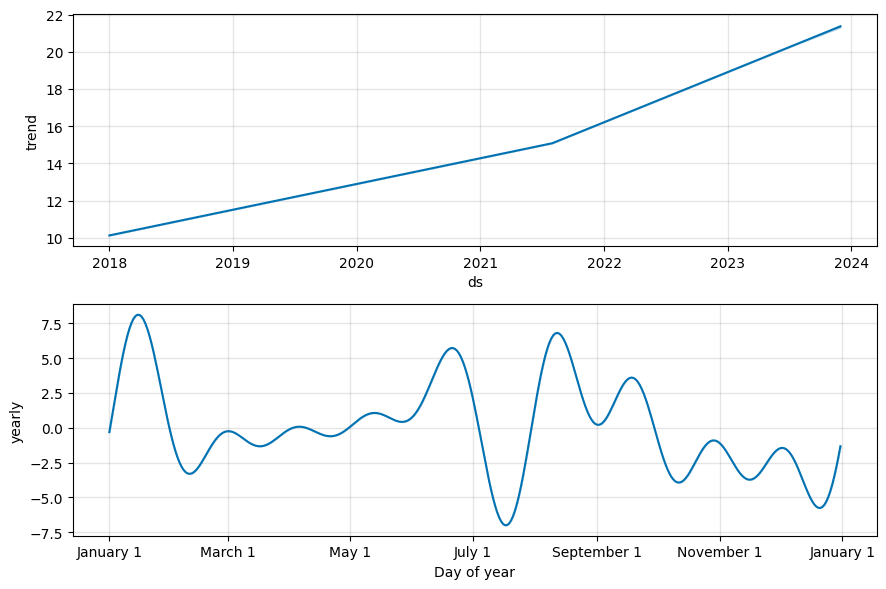
predictions.head()

结果（如下图），预计在 7 月、8 月见顶，随后在年底回落在 20%左右。

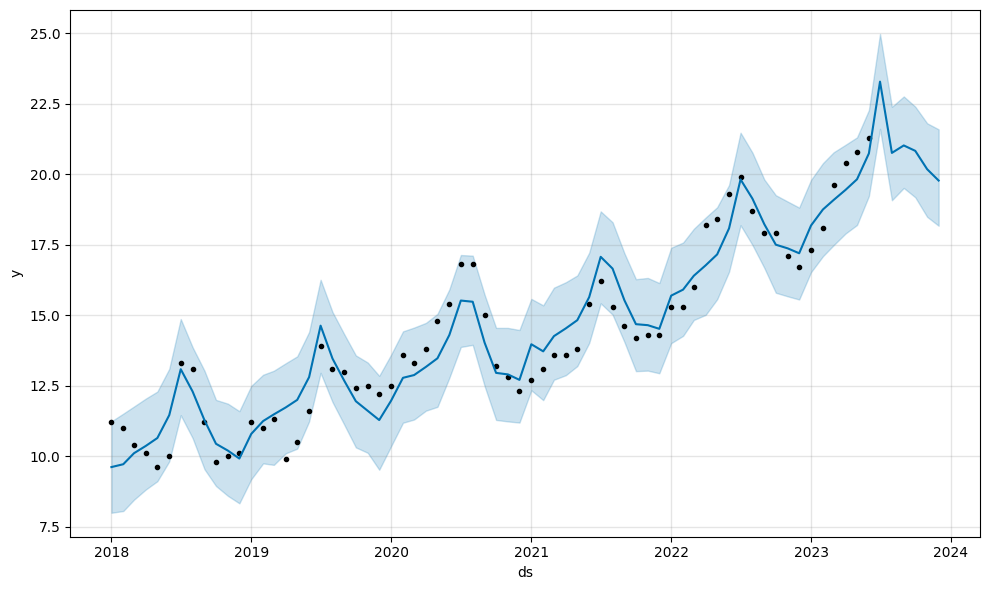
交叉检验

这里交叉检验非常重要，因为由于青年失业率是在 2018 年才存在的指标，仅仅有训练数据，训练误差并不能体现出相应的性能，要充分利用有限的数据，进行多次验证或者将测试集的比例增大，可以在统计学上提高算法的置信度。

预测显然不准确，但我们可以通过交叉验证衡量误差，尝试评估 12 个月范围内的预测性能，从第一个截止点的 24 个月训练数据开始，然后每 3 个月进行一次预测，评估结果和分析如下：

from prophet.diagnostics import cross_validation, performance_metrics
from prophet.plot import plot_cross_validation_metric

df_cv = cross_validation(model, initial='720 days', period='90 days', horizon = '365.25 days')

# Calculate evaluation metrics
res = performance_metrics(df_cv)

plot_cross_validation_metric(df_cv, metric= 'mape')
plot_cross_validation_metric(df_cv, metric= 'rmse')
plot_cross_validation_metric(df_cv, metric= 'mae')
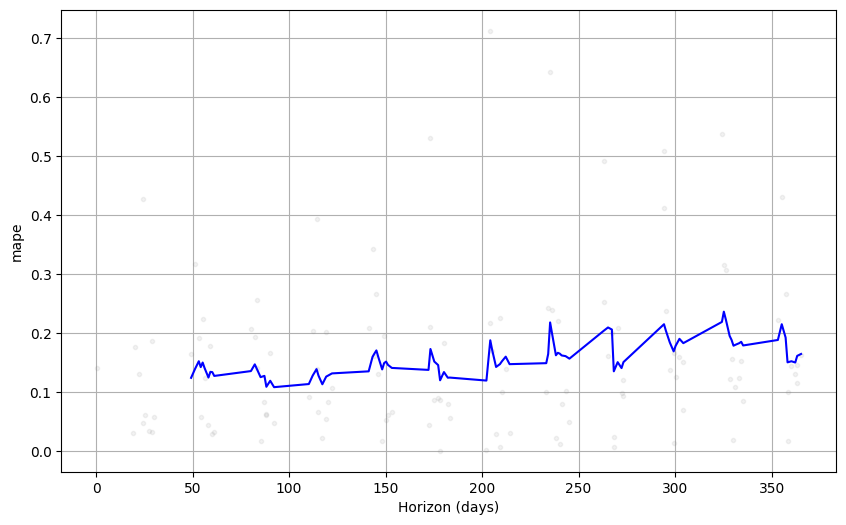
plot_cross_validation_metric(df_cv, metric= 'coverage')

平均绝对百分比（MAPE）误差计算预测值相对于实际值的百分比误差的平均值。在无异常的数据中表现良好，认为 200 日之前的误差较少。

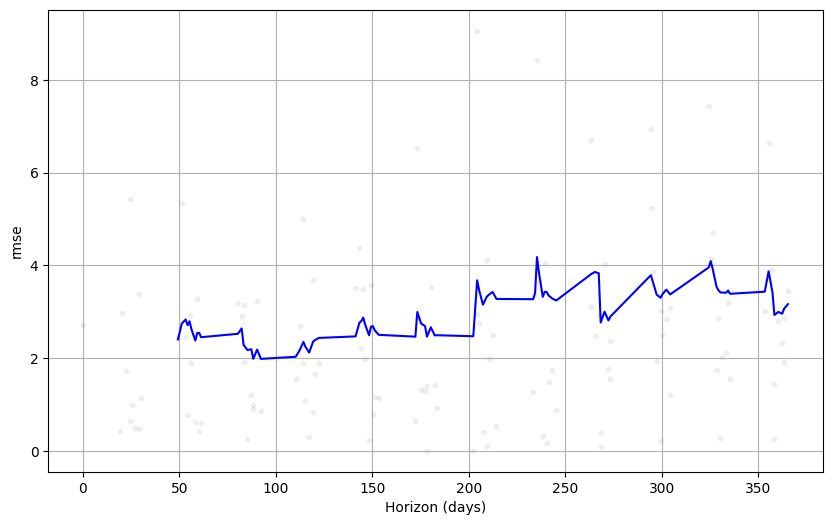
均方误差 (MSE)衡量预测值与实际值之间的平均平方差，对异常值敏感，200 日后的误差显著上涨接近翻倍。

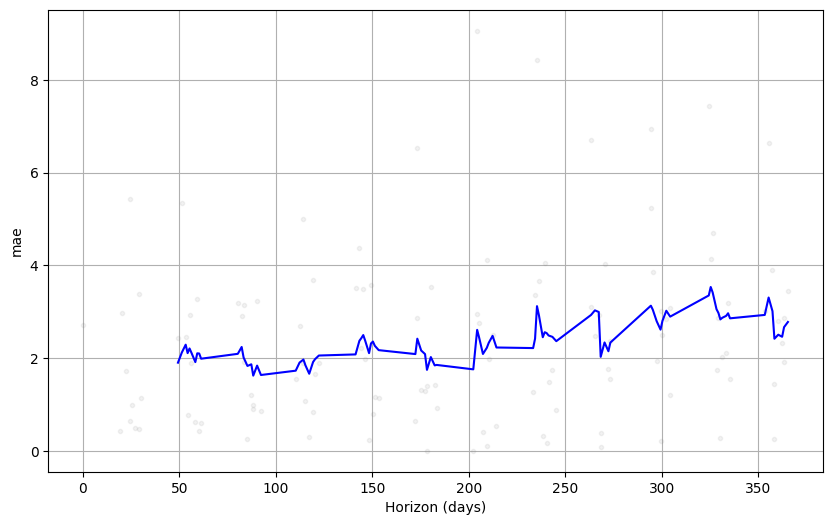
平均绝对误差 (MAE)是预测值与实际值之间的平均绝对差，关注误差的绝对大小。270 日前的误差理想。

覆盖率 (Coverage)评估置信区间的性能，覆盖率就是衡量这些置信区间是否能够包含实际值的比例。考虑到使用 95%的不确定性宽度（符合现实情况），所以半年内的测量偏差较少。

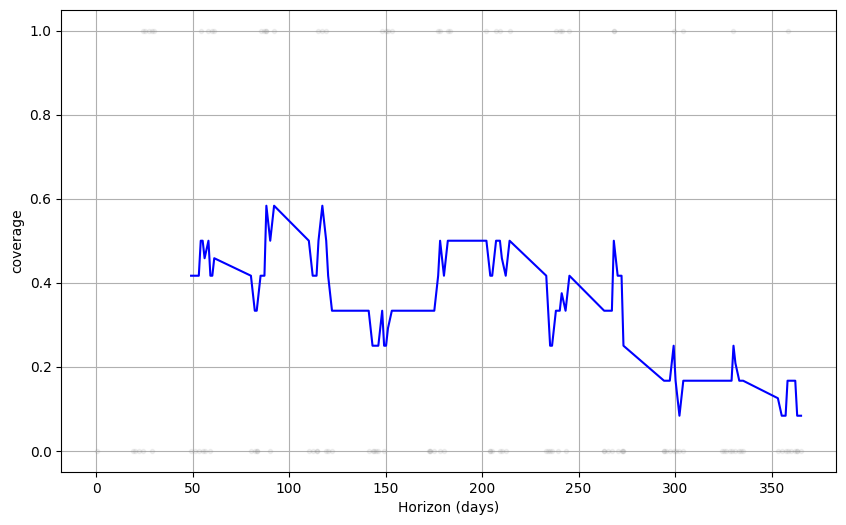
综上所述，其实通过 4 种不同方式的评估，考虑 180 日内预测结果是可信的。

分析

如下图，周期性和季节性非常符合现实：

1. 春招岗位较少，但持续时间的短，在过年后到 3 月初，2 月青年失业率平均下跌 2.7%，3-5 月失业率都有所降低

2. 秋招市场供应相比春招大，10-12 月的降低幅度比春招更大

3. 就业数据存在滞后性，需考虑企业招聘流程的时长，一般推前 1 个月为实际情况

为了体现相关性，取对数处理，使得变量之间的关联强度呈线性关系，这样能直接使用 Pearson 相关系数衡量：

np.log(df.loc[:, df.columns != 'date']).corr(method='pearson')

ln	National urban survey unemployment rate(%)	Urban survey unemployment rate in 31 large cities(%)	National urban survey unemployment rate for 16-24 year olds(%)	National urban survey unemployment rate for 25-59 year olds(%)
National urban survey unemployment rate(%)	1	0.869653	0.539167	0.828957
Urban survey unemployment rate in 31 large cities(%)	0.869653	1	0.754967	0.575193
National urban survey unemployment rate for 16-24 year olds(%)	0.539167	0.754967	1	0.01001
National urban survey unemployment rate for 25-59 year olds(%)	0.828957	0.575193	0.01001	1

注：经检验，p-value 都小于 0.05

值得注意的是，在所进行的行业研究中，我们观察到 31 个主要城市的失业率数据。在这些数据中，我们发现 16 至 24 岁年龄组的失业率与整体失业率之间的相关系数为 0.754967，而这一相关系数高于 25 至 59 岁年龄组之间的相关系数（0.57519）。这一现象提示我们，针对年轻人的岗位流失在大城市中似乎更为突出。

有趣的是，我们还发现 16 至 24 岁年龄组的失业率与 25 至 59 岁年龄组之间的失业率相关性极低，仅为 0.01001。这表明这两个年龄组的失业情况几乎没有显著关联。因此，有理由将青年失业视为一个独立的问题，而不是系统性或技术性失业的一部分。

反过来想，在周期性高峰选择不公开数据，考虑到市场的反身性，本身是一种公共政策下的市场干预。