November 16, 2023 · 4203 words · 9 min read

沪深300估值研究：岭回归、拉索回归和交叉检验

通过对沪深300的PE TTM数据和中国经济数据回归分析，揭示对于长期主义指数投资的有效性，经济基本面分析仍然有效，规模以上工业利润率、GDP平减指数、Shibor利率是值得关注的经济指标

岭回归和拉索回归

前言

在金融领域，使用时间序列预测宽基指数是困难的，由于数据是低维度的，没有外生性的因素，而在金融基础发达的地区，估值是相对稳定的，并反映经济基本面。本文着眼于沪深300指数，通过对其估值影响因素的研究，以期为投资者提供更深入的市场分析。我们将关注经济数据，探讨工业企业营业收入利润率、GDP平减指数、SHIBOR三个月利率等因素，并运用LM回归、残差分析、Bootstrap、岭回归、Lasso等方法进行深入研究，最终得出结论和相关建议。

数据结构

日期	滚动市盈率TTM	全要素生产率	外商直接投资	SHIBOR3个月	中国经济政策不确定性指数	工业企业营业收入利润率	GDP平减指数
10/31/2006	19.74	0.034142	59.9	2.6479	59.54	5.95	0.21
11/30/2006	24.63	0.034142	56.9	2.8054	57.29	6	0.21
12/31/2006	32.36	0.034142	87.6	2.8082	56.59	6.09	0.21
...	...	...	...	...	...	...	...

注：

截至到2019年12月最后一日，数据来源于万得Wind，部分季度指标的月数据用平均值补充。
GDP数据容易因”技术上的统计错误“而导致无法体现经济真实增长情况。
考虑到全社会的物价增长情况，而CPI中食品价格占比高，所以选用GDP平减指数，反映货币供应与货币需求的比例关系。

\text{GDP平减指数} = \frac{\text{名义GD}}{\text{真实GDP}}*100

GDP由CIGNX组成，其中中国的投资具有较高的权重，一般认为平减指数的同比增长和CPI同比增长高越多，说明投资价格上涨远超于消费价格上涨。
SHIBOR为上海银行间同业拆放利率，它包含着银行间的风险，所以不是真正意义的无风险利率，但其对市场真实利率更为敏感。
之所以不考虑就业数据，是因为失业率是一个滞后性很强的指标，CPI同理。

LM回归

我们使用LM回归来建立沪深300估值与经济指标的关系模型。具体回归方程如下：

data = read.csv("沪深300估值回归/沪深300估值回归数据.csv")


lm.fit = lm(
  log(滚动市盈率TTM) ~ log(全要素生产率) + log(外商直接投资) + log(SHIBOR3个月) + log(GDP平减指数) + log(中国经济政策不确定性指数) + log(工业企业营业收入利润率),
  data = data
)

summary(lm.fit)

通过回归结果，我们发现工业企业营业收入利润率、GDP平减指数和SHIBOR三个月利率对沪深300估值的影响具有统计显著性。

> summary(lm.fit)
Call:
lm(formula = log(滚动市盈率TTM) ~ log(全要素生产率) +
    log(外商直接投资) + log(SHIBOR3个月) + log(GDP平减指数) +
    log(中国经济政策不确定性指数) + log(工业企业营业收入利润率),
    data = data)

Residuals:
    Min      1Q  Median      3Q     Max
-0.7738 -0.1835  0.0037  0.1525  0.6529

Coefficients:
                              Estimate Std. Error t value Pr(>|t|)
(Intercept)                    0.07485    3.49408   0.021   0.9829
log(全要素生产率)             -0.23283    1.06685  -0.218   0.8275
log(外商直接投资)             -0.01321    0.08861  -0.149   0.8817
log(SHIBOR3个月)              -0.34985    0.07026  -4.979 1.71e-06 ***
log(GDP平减指数)              -0.77056    0.09593  -8.033 2.45e-13 ***
log(中国经济政策不确定性指数) -0.14295    0.07726  -1.850   0.0662 .
log(工业企业营业收入利润率)    1.49804    0.22976   6.520 9.81e-10 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2296 on 152 degrees of freedom
Multiple R-squared:  0.7252,	Adjusted R-squared:  0.7143
F-statistic: 66.84 on 6 and 152 DF,  p-value: < 2.2e-16

从 $R^2$ 和调整 $R^2$ 来看，两者都大于0.7，认为模型解释了回归中70%+的拟合数据，这是理想的情况。

这里的截距可能是一些不可量化的数据，如儒家文化圈下劳动人民的勤奋程度。

从t value来看，只有SHIBOR3个月、GDP平减指数、工业企业营业收入利润率三个变量呈现统计显著（95%置信区间）有参考意义。

结果显示影响沪深300估值最为明显的是工业企业营业收入利润率，其次是GDP平减指数和外商直接投资。

残差分析

我们进行残差分析，检验回归模型的拟合效果。残差分析包括残差与拟合图、残差的正态分布图、分布位置图以及残差和杠杆图。通过观察这些图表，我们可以判断回归模型是否符合OLS的假设。

残差等于观测值和相对应拟合值的差，那么理想中满足以下两点：

残差是独立不相关的，且均值为零
残差的方差是常数且满足正态分布

plot模型能直接输出四张残差图：

plot(lm.fit)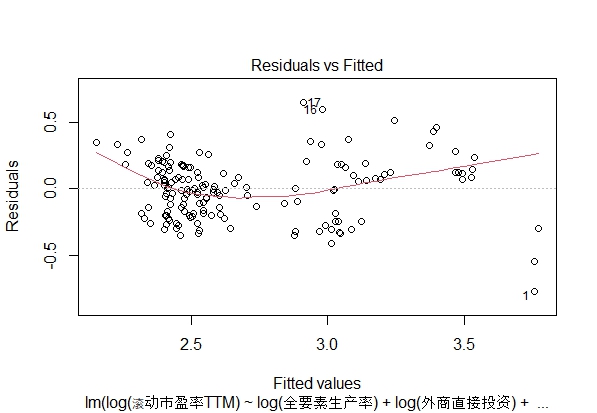

残差与拟合图

残差的期望接近于0，但右下角的三个异常值偏离了理想的残差，但对整体影响不大，拟合情况良好。

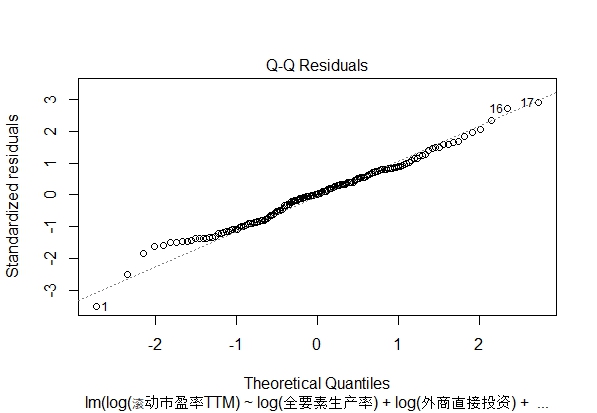
残差的正态分布图

残差的正态概率近似直线，说明符合OLS残差正态分布的假设。

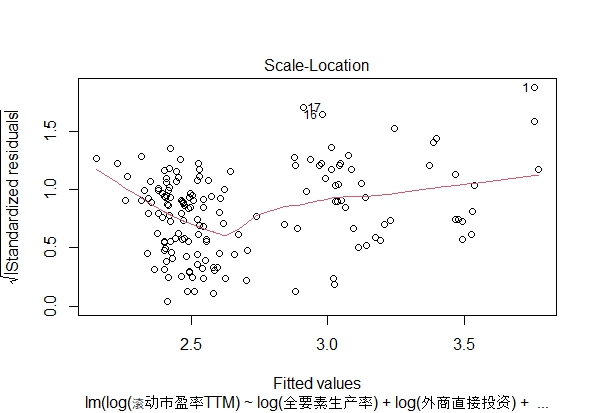
分布位置图

这是检查等方差（同方差）假设的方法，当 x 轴经过 2.7 左右时，残差开始沿 x 轴分布得更宽更平。由于残差分布得越来越宽和稀疏，红色平滑线不是水平的，说明残差并不完全沿变量范均匀分布。

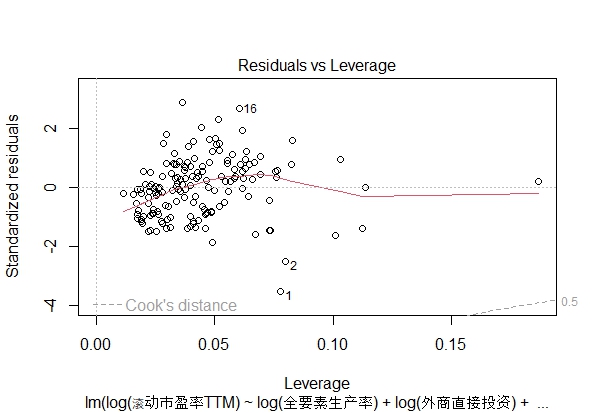
残差和杠杆图

所有的点都在Cook's distance之外，说明上述观察到三个异常值实际上并未造成严重误差。

考虑到2008年金融危机的经济数据相对于大部分时间是异常值，但基于实证，不能因此剔除数据，所以残差分析的结论是该log-log模型的残差符合OLS的假设，有参考价值。

Bootstrap

为了验证模型的性能，我们使用Bootstrap方法进行重抽样。通过重抽样，我们计算得到模型参数的偏差，并观察其分布情况，以确保模型的可靠性。

Bootstrap和Monte Carlo的差异主要是，Monte Carlo重抽设定好的总体分布模型，是无偏的，而估计值为整体估计，而Bootstrap重抽观察到的基于真实数据的样本分布

首先构建函数，subset = index能指定要在拟合过程中使用的观测子集，函数返回估计值。

# Bootstrap
library(boot)
boot.fn <- function(data, index) {
  return(coef(
    lm(
      log(滚动市盈率TTM) ~ log(全要素生产率) + log(外商直接投资) + log(SHIBOR3个月) + log(GDP平减指数) + log(中国经济政策不确定性指数) + log(工业企业营业收入利润率),
      data = data,
      subset = index
    )
  ))
}
set.seed(1)
boot.fn(data, sample(300, 300, replace = T)) #调用函数重抽样，每次结果都有较大相差
boot(data, boot.fn, 1000)

使用bootstrap重抽样1000次。

> boot(data, boot.fn, 1000)
ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = data, statistic = boot.fn, R = 1000)


Bootstrap Statistics :
       original       bias    std. error
t1*  0.07485309 -0.121315553  3.30482903
t2* -0.23283009 -0.023225896  1.01562531
t3* -0.01321231  0.006689070  0.08538500
t4* -0.34985328  0.003010512  0.07259779
t5* -0.77056078 -0.013000676  0.12916912
t6* -0.14294676  0.002778872  0.08577070
t7*  1.49803851 -0.006526517  0.22630775

bootresults <- boot(data, boot.fn, 1000)
plot(bootresults)
boot.ci(boot.out = bootresults, type = c("norm", "basic", "perc", "bca"))

> boot.ci(boot.out = bootresults, type = c("norm", "basic", "perc", "bca"))
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 1000 bootstrap replicates

CALL :
boot.ci(boot.out = bootresults, type = c("norm", "basic", "perc",
    "bca"))

Intervals :
Level      Normal              Basic
95%   (-6.3676,  6.7592 )   (-6.5270,  6.7322 )

Level     Percentile            BCa
95%   (-6.5825,  6.6767 )   (-6.4860,  6.8511 )
Calculations and Intervals on Original Scale

正则化

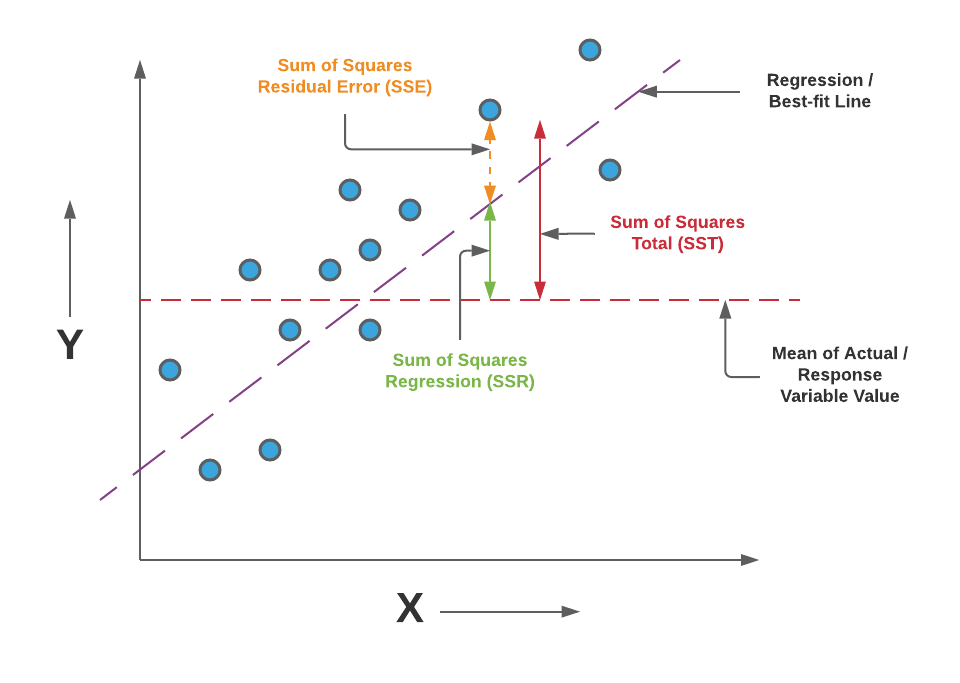
首先回顾RSS(Residual Sum of Squares)，

RSS = \sum_{i=1}^{n}(y_i - \beta_0 - \sum_{j=1}^{p}\beta_j x_{ij})^2

在Ridge回归中的回归系数 $\hat{\beta}^R$ 需要最小化

RSS + l_2 norm = RSS + \lambda \sum^{p}_{j=1} \beta^2_j

而Lasso回归系数 $\hat{\beta}^L$ 需要最小化

RSS + l_1 norm = RSS + \lambda \sum^{p}_{j=1} |\beta_j|

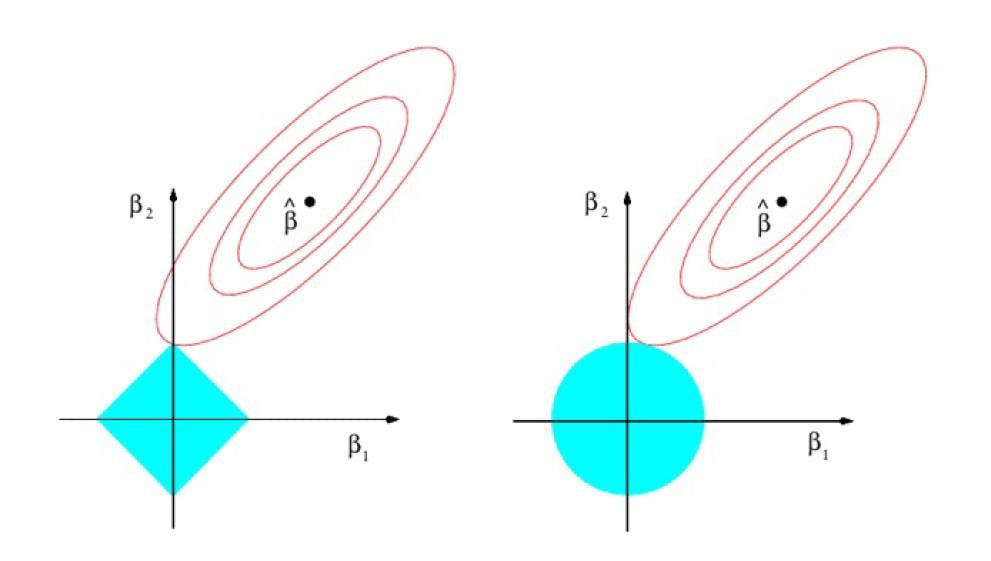
图形化表示如下

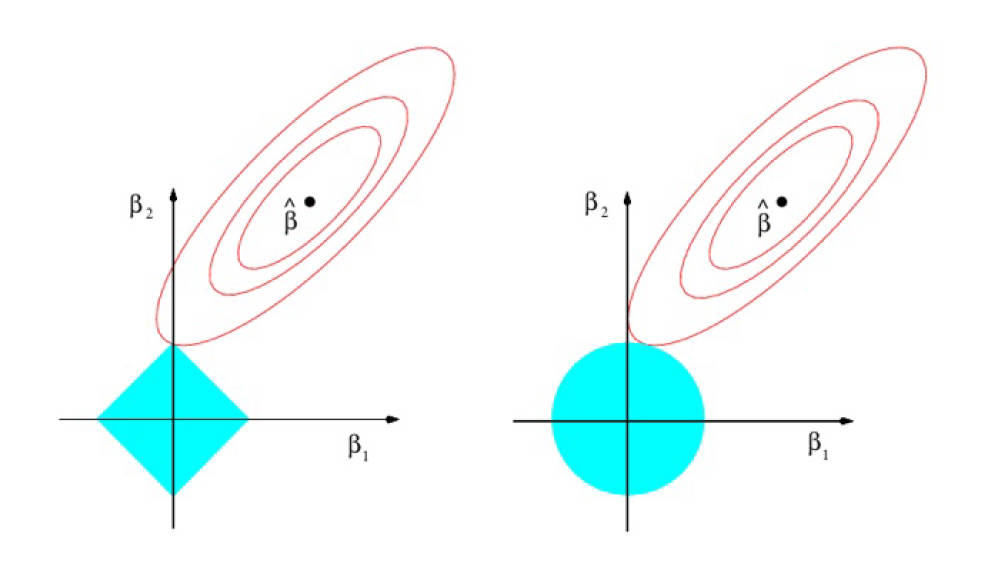
Lasso左，Ridge右，蓝色区域为约束区域，红色圆表示RSS

Lasso约束区域在每个轴上会有拐角，如果椭圆和它相交，那么回归系数就是0，所以如果椭圆距离较远，有可能多个系数同时为0，以此实现惩罚的效果。

我们采用岭回归和Lasso回归来进一步优化模型，考虑到可能存在多重共线性的情况。通过交叉验证和正则化参数的选择，我们得到最优的模型，并观察其在测试集上的表现。

考虑到选择的变量都是外生性的经济指标，无一是无关紧要的，且在现实世界极有可能有多重共线性的情况，岭回归是最佳的解决方案。

# Ridge
library(glmnet)
x = model.matrix(
  log(滚动市盈率TTM) ~ log(全要素生产率) + log(外商直接投资) + log(SHIBOR3个月) + log(GDP平减指数) + log(中国经济政策不确定性指数) + log(工业企业营业收入利润率),
  data = data
)[, -1]
y = log(data$滚动市盈率TTM)
grid <- 10 ^ seq(10,-2, length = 100)
ridge.mod <- glmnet(x, y, alpha = 0, lambda = grid)
plot(ridge.mod, label = TRUE)

glmnet中alpha=0拟合岭回归，alpha=1为lasso回归

cv_fit <- cv.glmnet(x, y, alpha = 0, nlambda = 1000)

plot(cv_fit)

cv_fit$lambda.min
fit <- glmnet(x, y, alpha = 0, lambda = cv_fit$lambda.min)
fit$beta

而最小MSE误差的lambda为0.03403989，外商直接投资FDI的系数接近0，说明长期来看杀估值和外资撤走并没直接联系。

> fit$beta
6 x 1 sparse Matrix of class "dgCMatrix"
                                       s0
log(全要素生产率)             -0.68876215
log(外商直接投资)             -0.07225806
log(SHIBOR3个月)              -0.31431993
log(GDP平减指数)              -0.66421314
log(中国经济政策不确定性指数) -0.17979614
log(工业企业营业收入利润率)    1.34609022

有时候可以选用相对宽松的条件，尽可能避免过拟合，所以将lambda调为1倍标准差值，lambda值为0.1601994。

cv_fit$lambda.1se
fit <- glmnet(x, y, alpha = 0, lambda = cv_fit$lambda.1se)
fit$beta

> fit$beta
6 x 1 sparse Matrix of class "dgCMatrix"
                                      s0
log(全要素生产率)             -1.1920025
log(外商直接投资)             -0.1548118
log(SHIBOR3个月)              -0.2311252
log(GDP平减指数)              -0.4897630
log(中国经济政策不确定性指数) -0.2050566
log(工业企业营业收入利润率)    0.9614087

在简单log-log的回归中，全要素生产率变量并没呈现统计显著，且系数为-0.23283，而岭回归的系数是-0.68876215和**-1.1920025**。

细心的人会发现这里没有显著性测试，这是非常巧妙的：在L1和L2惩罚回归模型，我们不会得到系数的 CI 或标准误差，在决定lambda后，这些估值系数是无偏的，因为它们没有意义，应该进一步交叉检验。

全要素生产率考虑的是不包括资本和劳动力等外来输入，其他所有影响产出的要素，即纯技术进步带来的生产率的增长。这其实非常符合现实，国有企业长期垄断，生产效率低下，而民企生产效率相对较高，竞争异常激烈。

使用linearRidge用 Cule et al (2012)的半自动选择方法选择lambda，all.coef帮助我们返回所有岭回归的惩罚结果，上文已经拟合过，所以选FALSE。

# linearRidge
ridge_model = linearRidge(
  log(滚动市盈率TTM) ~ log(全要素生产率) + log(外商直接投资) + log(SHIBOR3个月) + log(GDP平减指数) + log(中国经济政策不确定性指数) + log(工业企业营业收入利润率),
  data = data,
  all.coef = FALSE
)
summary(ridge_model)

> summary(ridge_model)
Call:
linearRidge(formula = log(滚动市盈率TTM) ~ log(全要素生产率) +
    log(外商直接投资) + log(SHIBOR3个月) + log(GDP平减指数) +
    log(中国经济政策不确定性指数) + log(工业企业营业收入利润率),
    data = data, all.coef = FALSE)


Coefficients:
                              Estimate Scaled estimate Std. Error (scaled) t value (scaled) Pr(>|t|)
(Intercept)                   -0.25466              NA                  NA               NA       NA
log(全要素生产率)             -0.41513        -0.10449             0.25563            0.409   0.6827
log(外商直接投资)             -0.03634        -0.12846             0.29396            0.437   0.6621
log(SHIBOR3个月)              -0.33763        -1.53578             0.29679            5.175 2.28e-07 ***
log(GDP平减指数)              -0.72884        -3.14983             0.36743            8.573  < 2e-16 ***
log(中国经济政策不确定性指数) -0.15889        -0.75261             0.33044            2.278   0.0228 *
log(工业企业营业收入利润率)    1.44586         1.66397             0.25161            6.613 3.76e-11 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Ridge parameter: 0.02611379, chosen automatically, computed using 4 PCs

Degrees of freedom: model 5.705 , variance 5.432 , residual 5.977

结果上看FDI的系数还是接近于零，

一般来说，正则化的目的是在准确性和简单性之间取得平衡。函数cv.glmnet() 可以找到给出最简单模型的 lambda 值，该值也在最佳 lambda 值的一个标准误差之内。

K-fold 交叉验证


# 10-fold cross-validation
library(dplyr)
library(purrr)
library(modelr)

cv1 <- crossv_kfold(data, k = 5)
models <- map(cv1$train, ~ ridge_model)
summary(map2_dbl(models, cv1$test, modelr::mape))

MAPE指平均绝对百分比误差，它是一种相对度量，方便直接衡量误差。

> summary(map2_dbl(models, cv1$test, modelr::mape))
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
0.05702 0.06184 0.06563 0.06613 0.06846 0.07769

从MAPE的分位值分布来看，该岭回归拟合优秀，并没有过拟合。

Lasso

Lasso回归会降低了系数，反而增强了惩罚，一般将alpha调到1（惩罚最严厉），通过正则化方法，我们得到了更为简化的模型，进一步提高了模型的泛化能力。


#lasso
lasso.mod <- glmnet(x, y, alpha = 1, lambda = 10 ^ seq(10,-2, length = 100))
plot(lasso.mod, label = TRUE)

cv_fit2 <- cv.glmnet(x, y, alpha = 1, nlambda = 1000)

plot(cv_fit2)
cv_fit2$lambda.min
fit2 <- glmnet(x, y, alpha = 1, lambda = cv_fit2$lambda.min)
fit2$beta

cv_fit2$lambda.1se
fit2 <- glmnet(x, y, alpha = 1, lambda = cv_fit2$lambda.1se)
fit2$beta

相对应的，在最小lambda的情况下，全要素生产率、外商直接投资、中国经济政策不确定性指数的系数接近为0，在一倍标准差的lambda的情况下，以上三个变量的回归系数变为0，而其余变量的回归系数只有GDP平减指数增长。

> cv_fit2$lambda.min
[1] 0.005178099
> fit2 <- glmnet(x, y, alpha = 1, lambda = cv_fit2$lambda.min)
> fit2$beta
6 x 1 sparse Matrix of class "dgCMatrix"
                                         s0
log(全要素生产率)             -0.0377279697
log(外商直接投资)             -0.0005575801
log(SHIBOR3个月)              -0.3273320465
log(GDP平减指数)              -0.7860965804
log(中国经济政策不确定性指数) -0.1224871859
log(工业企业营业收入利润率)    1.3933377085
> cv_fit2$lambda.1se
[1] 0.03935965
> fit2 <- glmnet(x, y, alpha = 1, lambda = cv_fit2$lambda.1se)
> fit2$beta
6 x 1 sparse Matrix of class "dgCMatrix"
                                      s0
log(全要素生产率)              .
log(外商直接投资)              .
log(SHIBOR3个月)              -0.1421765
log(GDP平减指数)              -0.8387103
log(中国经济政策不确定性指数)  .
log(工业企业营业收入利润率)    0.6895035

曾想过是否能直接剔除掉这些”非关键变量“再进行回归？是不能的，否则就犯了遗漏变量偏差这一根本错误！理论上应加入的外生性变量都要加入进去。

塔勒布曾讲述统计学的一常见错误，不统计显著不是结论，换而言之，不能过度解读“平凡的数据”。

结论

工业企业营业收入利润率为推动沪深300估值的关键因素，其次是GDP平减指数、SHIBOR三个月利率，也就是整体通胀水平和短期利率为辅。

沪深300的估值长期和工业企业营业收入利润率强相关，是经得住考验的“经济晴雨表”指数，宽松的货币政策对推高市场估值是有效的，而媒体常谈的政策不确定性和外资撤离因素有待进一步验证。

对于长期指数投资者，更应该审视宏观经济和行业竞争格局，而不是市场上的风吹草动。

参考来源

An Introduction to Statistical Learning with R(作者非常喜欢的统计学书)

Last Updated: March 6, 2024

CC BY-NC-SA 4.0