肥尾效应:风险社会的游戏规则
分布是静态的,但事实是非线性且连续性的。
规则
Ulrich Beck《风险社会》的背景:自工业社会以来,社会生产出不平等财富却被合法地被分配,面临现代性自反性本身的制度性危机。
分布
对于亚指数类分布来说,破产更可能来自某次极端事件,而不是一系列糟糕事件的累积。这一逻辑在 20 世纪早期由精算学家菲利普·伦德伯格提出,到 20 世纪 30 年代由哈拉尔德·克拉默整理完善,对传统风险管理理论形成了巨大挑战。但如今,很多经济学家完全忽视了这一点。从保险的角度讲,分散化有效的前提是,损失更可能来自一系列事件而不是单个事件。
灾难原则:在存在巨大灾难风险的情况下,永久不要出售一款损失无上限的保险。
分布的中间部分完全是噪音,并不包含任何实证的信息。
为什么一百万次的观测,大数定律会“无效”?100 万次的肯定性观测不如 1 次否定,Monte Carlo method 问题又在哪?波普尔的非对称性。
大数定理即便存在,奏效速度很慢。
样本均值大概率不会贴近分布的实际均值,尤其是遇到偏态分布(或单尾分布)时,均值的估计量会持续被小样本效应主导(即被低估或高估)。
方差和标准差这样的统计量是不可用的。
贝塔系数、夏普比率和其他惯用的金融统计量均无参考意义。
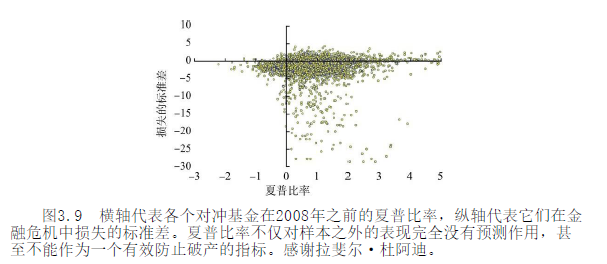
实际上,所有经济金融领域的变量和证券回报都是厚尾分布的。我们统计了超过 4 万只证券的时间序列,没有一只满足薄尾分布,这也是经济金融研究中最大的误区。
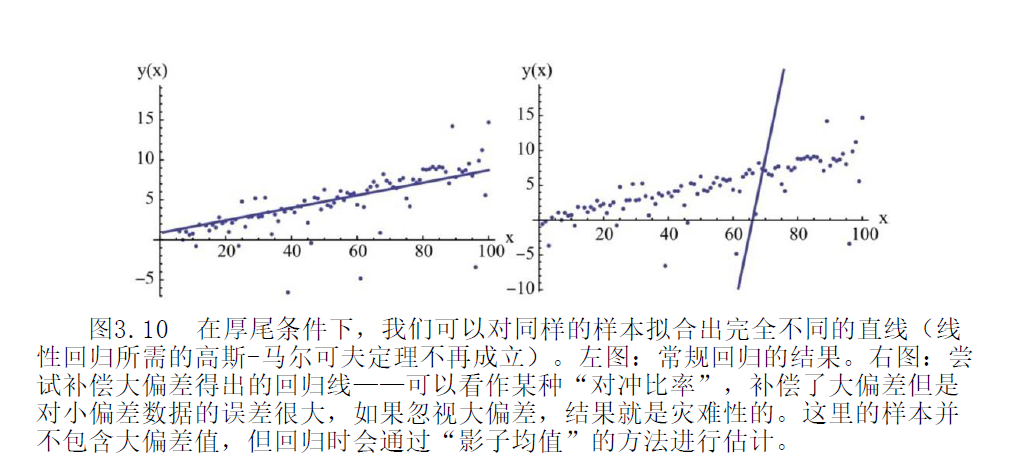
由于厚尾的小样本效应,回归样本内的决定系数远远大于真实值。当随机变量方差无穷大的时候,应该等于 0。但是,因为回归样本量必然有限,会给出高于 0 的欺骗性结果。因此,在厚尾条件下,不仅完全没有意义,还会因为高估时不时产生十足的欺骗作用(就像智商研究一样)。
我们要面临一个现实世界中的问题:如果没有靠谱的统计量怎么办?那最好还是在家里待着,我们不能把自己暴露在脆弱性的风险之下。不过,如果可以锁定最大损失,我们就可以做出承担风险的决策。
作者此前和认知语言学家兼科普作家斯蒂芬·平克有过一次争论:从最近的数据变化中得出结论(或归纳出理论)并不可行,除非满足一定的置信度条件,这就需要在厚尾条件下有更多的数据(和缓慢大数定律的逻辑相同)。因此,根据最近一年或十年非自然死亡人数的下降,得出“暴力致死行为有所下降”这样的结论并不科学。科学论断之所以和奇闻逸事不同,是因为它对样本外发生的事情有预测作用,统计意义显著。
这里我再次强调,统计意义不显著的结论并不算真正的科学。不过,说暴力行为在某次观察中上升则可能是一个严谨的科学论断。在薄尾的情况下解读描述性统计量的做法可能是可以接受的(因为显著结论所需的样本量不大),但在厚尾情况下肯定不行,除非包含尾部信息的超大偏差重复出现在样本集中。
在《随机漫步的傻瓜》一书中,某人被问,到月底市场更有可能上涨还是下跌?他表示上涨的可能性更大,但后来发现,他在押注市场下跌。对不懂概率的人来说,这似乎很矛盾,但是对交易员来说再正常不过了,尤其是在非标准分布的条件下(确实,市场更有可能上涨,但如果下跌会跌得更多)。这个例子表明,人们常常混淆预测和风险敞口(预测的结果是二元的,而风险敞口的结果更多元,取决于整个分布的状态)。在这个例子中,一个非常基本的错误是,将发生概率理解为单个数字而非分布结果,而在进一步研究之后,我们会发现很多并不明显或不为人知的类似的悖论式问题。简单来说,作者认为,将“概率”作为最终标的,甚至作为决策的“基础”来讨论并不严谨。
幼稚的经验主义:不应该把埃博拉病毒和从梯子上跌落进行对比。让我们通过一个真实世界的例子来阐述用薄尾思维衡量肥尾事件带来的问题。有时候,人们会引用所谓的“经验”数据来说明我们不该担心埃博拉病毒,因为 2016 年只有两个美国人死于埃博拉病毒。他们认为,从死亡数字看,我们更应该担心死于糖尿病或躺在床上。但如果我们从尾部的角度思考,假设有一天报纸报道突然死了 20 亿人,他们更可能死于埃博拉病毒还是死于吸烟、糖尿病或躺在床上呢?
记得有个西方的媒体在今年初采访某银行的 economist 评价大陆放开疫情管控的结果,每年死于糖尿病和心脑血管病等慢性疾病的每年就多达 300 万,而放开疫情“只会死少于 30 万”,根据已有的传播率和死亡率。
我当时一听就觉得这人是被传统金融/经济模型误导的专业人士,这听起来很有道理,所有数据都有迹可查,慢性疾病往往是显性的,众多人所知,处于分布的中间地段,因为他们不是急性致死的,或没有彻底康复的可能性,它最糟糕的结果无非是预期寿命的减少,而不是造成大规模的死亡,被认为是薄尾的。
而放开管控的致死可能是未知的,考虑到人均医疗资源的微小以及医疗负荷,清零和动态防疫对于大陆而言是对死亡率的可控范围,它不是黑天鹅,但它引发灾害的预期并不准确,尽管有“显著”的统计数据表明不会造成过多的死亡病例,那最后得出大陆关于放开管控的分布不明的结论。
不少人喜欢用其他国家和地区的经验进行对比,二阶矩可能相差甚远,在存在极端情况下,考虑到更多的社会因素(环境不可控),分布更可能变成肥尾,更不应该去对比厚尾变量和薄尾变量,统计显著仅局限于对应的 OLS 回归和特定条件,必须弄清楚现实的分布。
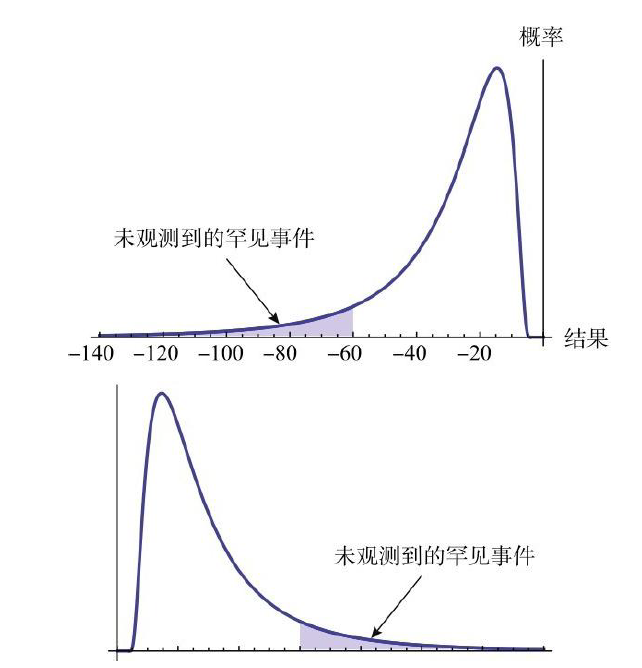
牛市预期的破产概率、气候变暖人类生存的概率、恐怖主义动乱的概率等等。
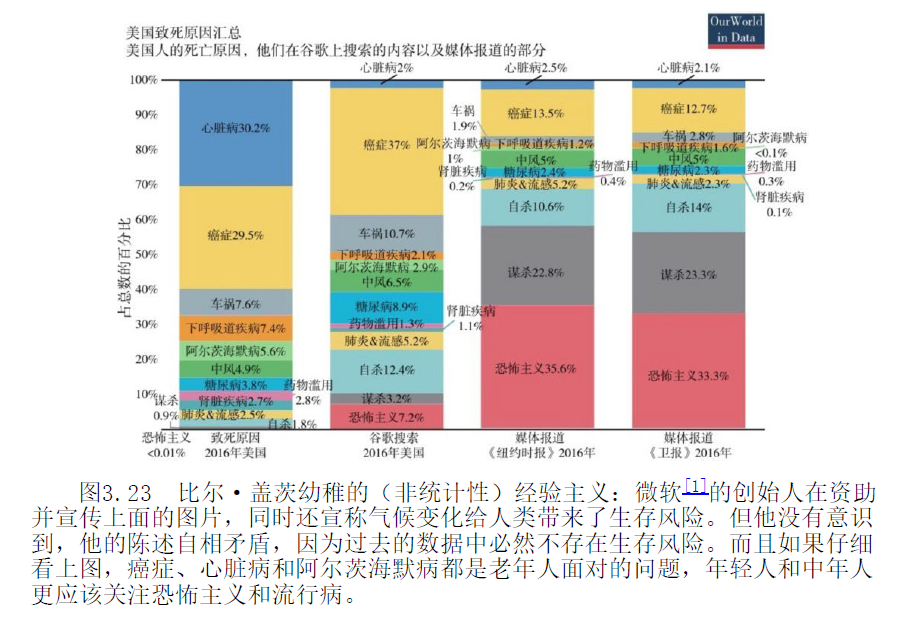
恐惧带来安全,经验主义根于认知偏差和“实证”。
不少人都会讲历史如何相似,大概这就是幼稚的“经验主义”和历史决定论的贫困。
涂尔干的《自杀论》,不论自杀是利己还是利他,或受怎样的社会背景和宗教,一个社会的自杀率是稳定的,往往与人和社会的连结程度有关,他们作为独立事件和社会事实,是不会传染的。
而 covid-19 毫无疑问,传染性对于社会死亡个案和概率就已经不是独立事件,而且是指数级的威胁,个体的感染会增加集体的死亡率,所以这就是倍增的肥尾。
帕累托分布
它的三阶中心矩即峰度:
一眼就能知道这是一个非常不稳定的值,实际的金融资产样本偏差往往非常大,二阶矩的稳定性也无从而知,那样就无法评估方差,现实中的峰度和方差可能是无限大的,在有限的样本中自然无法得到极限值。
所以做空波动率一定是被高估的,分布的左偏往往是有足够多的样本和可预测的,而右偏的尾部波动率则是被低估的,波普尔的非对称性表现之一,即证实和证伪的不对称,表现在市场逻辑上过去和未来的逻辑不对称。
定义发生的概率为
当,,只要有极小的可能,的数据就不是高斯分布。
只要出现超过就可以拒绝高斯分布的假设。
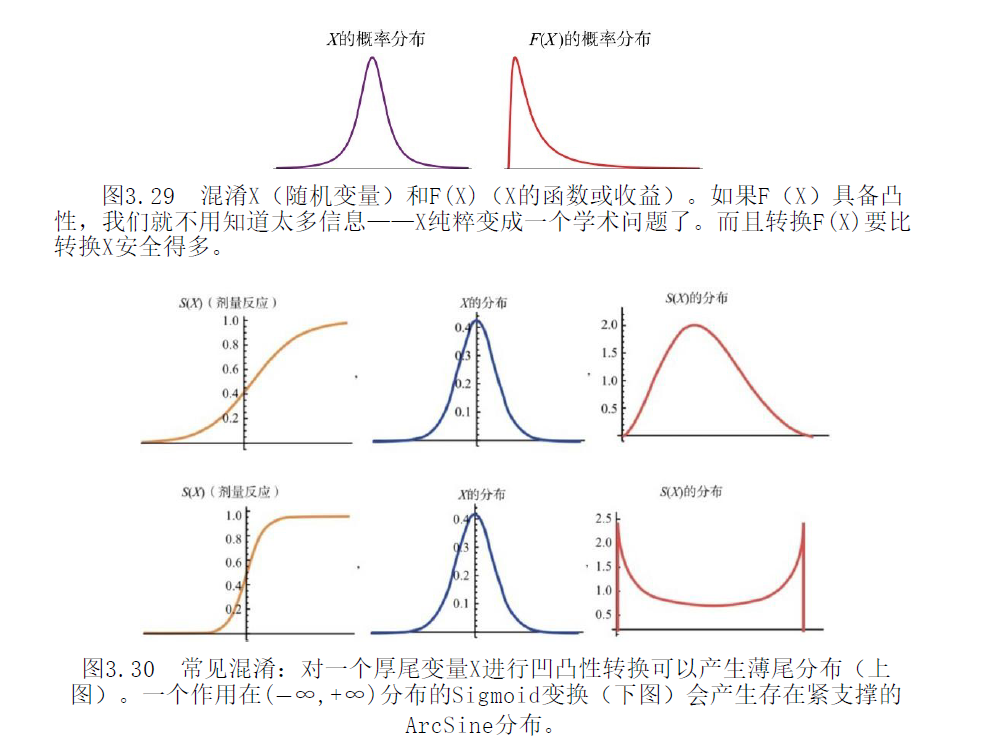
现实中是不可控的,但部分可控。
现实中人们过于关注(预测的目标),无法考虑到小概率事件,在厚尾分布,是最终影响的结果。
| 凸性 | 凹性 | |
|---|---|---|
| 性质 | 反脆弱 | 脆弱 |
| 和 | 了解 风险敞口 | 了解 x |
| 收益函数 | 凸函数 | 凹函数 |
| 波动率决策 | 做多变动率 | 做空变动率 |
| 预测 | “糟糕”的预测(薄尾) | 肥尾 |
Note. 预测指同平均数和方差下的波动率的聚集程度,即使结果正确,肥尾仍然暴露巨大且不对称的风险。
疫情管控的放松潜在出现大规模死亡事件,个体的感染必然影响其他人,财政支出、管控政策、医疗负荷等等,这和破产非常相似,这场“人传人”的游戏如下图:
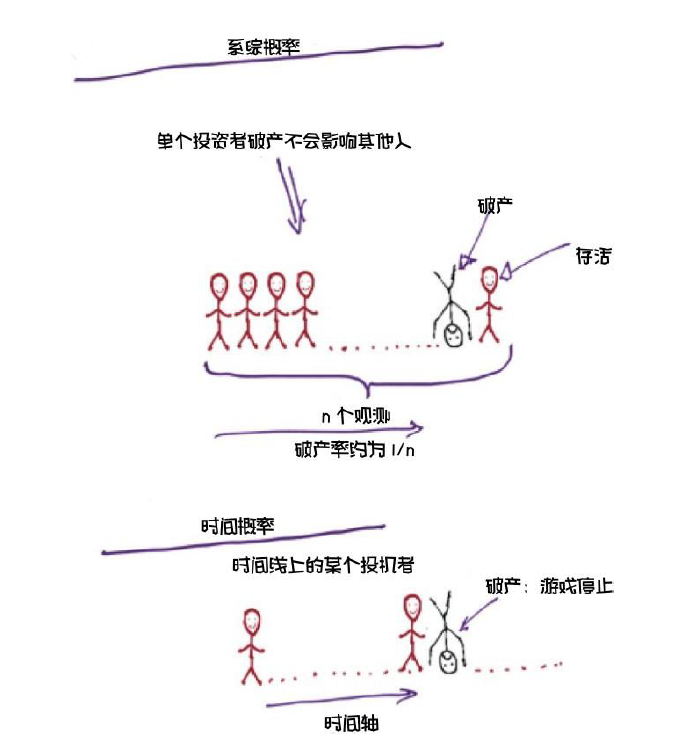
一般来说,投机过热是金融泡沫的迹象,大多数政府选择积极的资本管制政策吸引投资,打击杠杆化的投机活动,投机往往是个体受市场的正反馈,进入“谁是最大傻瓜”的游戏,每个投资者最终承担的风险的上限是本金,不会影响到其他人;对于投机者和新兴科技公司而言,投机者为了追逐趋势选择杠杆账户,新兴科技企业为了避税和扩张发展,往往背负一定的债务,当信贷扩张且宽松时,企业可以用一些缺乏流动性的抵押品抵押给银行,(省略),破产由股东、债权人、金融中介、客户等多方损失构成,它会造成另一个负反馈,市场中更少的流动性和更高的资产折价,挤兑风险和避险意识。
每个幸存下来的风险承担者都理解这一点。沃伦·巴菲特理解这一点,高盛集团也理解这一点,他们想要的不是极小的风险,而是完全杜绝风险,因为这才是一家公司能够存活 20 年、30 年甚至 100 年的关键。对尾部风险的态度解释了高盛 149 年来长盛不衰的原因——它以无限责任的合伙企业的形式运行了 130 年,然后在转型为银行后的 2009 年侥幸逃生。这一条并没有被写进决策理论的教科书,但是我们(风险共担者)每天都在练习。我们参与游戏,根据我们期望的寿命,考量重复风险暴露会在多大程度上降低我们的预期寿命。
事实上尾部风险不是可再生资源,尾部事件的叠加造成的是死亡本身。
在市场中,存活是最优先的规则。
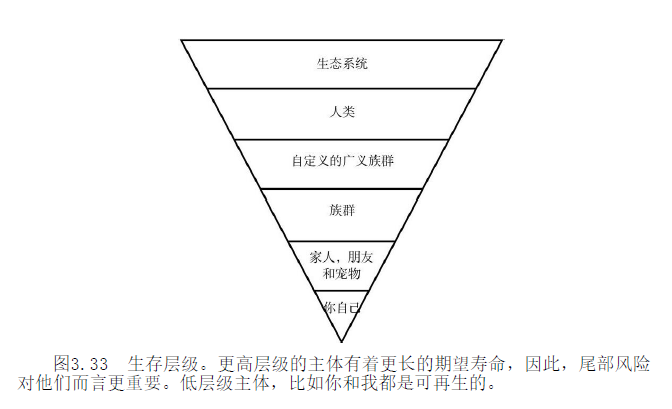
留一个猜想:僭主制度、军国主义也是类似的倒三角形层级,政府和国家在社群之上,集体主义的底层逻辑是否构成社会有机体论更长远的预期寿命?
待补充/填坑,未完待续
CC BY-NC-SA 4.0